Mechanical Insulation Design Guide
Introduction
Within This Page
This section of the Mechanical Insulation Design Guide offers a collection of information and data useful to designers and end users of mechanical insulation systems. The section contains some simple tools that allow the calculation of heat flow and surface temperatures. Discussion of and links to other, more sophisticated software programs for performing these calculations also are included.
Estimating Heat Loss / Heat Gain
Steady-state, one-dimensional heat flow through insulation systems is governed by Fourier's law (equation #1) below:
|
q = - k·A·dT/dx |
(1) |
where:
q = rate of heat flow, Btu/hr.
k = thermal conductivity of the insulation material, Btu-in/h ft2°F
A = cross-sectional area normal to heat flow, ft2
dT/dx = temperature gradient, °F/in
For flat geometry of finite thickness, the equation (#2) reduces to:
|
q = k ·A· (T1–T2)/X |
(2) |
where:
X = thickness of the insulation, in.
For cylindrical geometry, the equation (#3) becomes:
|
q = k·A2·(T1–T2)/(r2·ln (r2/r1)) |
(3) |
where:
A2= area of outer surface, ft2
r2 = outer radius, in
r1 = inner radius, in
The term r2 in (r2/r1) is sometimes called the "equivalent thickness" of the insulation layer. Equivalent thickness is that thickness of insulation that, if installed on a flat surface, would yield a heat flux equal to that at the outer surface of the cylindrical geometry.
Heat transfer from surfaces is a combination of convection and radiation. Usually, it is assumed that these modes are additive, and therefore a combined surface coefficient can be used to estimate the heat flow to/from a surface (equation #4):
|
hs = hc + hr |
(4) |
where:
hs = combined surface coefficient, Btu/h ft2 °F
hc = convection coefficient, Btu/h ft2 °F
hr = radiation coefficient, Btu/h ft2 °F
Assuming the radiant environment is equal to the temperature of the ambient air, the heat loss/gain at a surface can be calculated (equation #5):
|
q = hs·A·(Tsurf–Tamb) |
(5) |
The radiation coefficient is usually estimated as (equation #6):
|
hr = ε·σ·(Tsurf4 –Tamb4)/(Tsurf–Tamb) |
(6) |
where:
ε = emittance of the surface
σ = Stephen-Boltzmann constant (=0.1714 x 10-8 Btu/(h·ft2·°R4)
Tx = Temperature, °R
The emittance (or emissivity) of the surface is defined as the ratio of radiation emitted by the surface to the radiation emitted by a black body at the same temperature. Emittance is a function of the material, its surface condition, and its temperature. The approximate emittance of commonly used materials is given in Table 1.
Table 1. Emittance Data of Commonly Used Materials
| Material | Emittance (~80 °F) |
|---|---|
| All service jacket | 0.9 |
| Aluminum, anodized | 0.8 |
| Aluminum, commercial sheet | 0.1 |
| Aluminum, embossed | 0.2 |
| Aluminum, oxidized | 0.1–0.2 |
| Aluminum, polished | 0.04 |
| Aluminum paint | 0.5 |
| Aluminum-zinc coated steel | 0.06 |
| Canvas | 0.7–0.9 |
| Colored mastic | 0.9 |
| Copper, highly polished | 0.03 |
| Copper, oxidized | 0.8 |
| Elastomeric or polyisobutylene | 0.9 |
| Galvanized steel, dipped or dull | 0.3 |
| Galvanized steel, new, bright | 0.1 |
| Iron or steel | 0.8 |
| Painted metal | 0.8 |
| Plastic pipe or jacket (PVC, PVDC, or PET) | 0.9 |
| Roofing felt and black mastic | 0.9 |
| Rubber | 0.9 |
| Silicon impregnated fiberglass fabric | 0.9 |
| Stainless steel, new, cleaned | 0.2 |
©American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.
Convection is energy transport by the combined action of heat conduction, energy storage, and mixing action. It is classified as either forced convection (when the mixing motion is induced by some external agency) or natural convection (when the mixing action takes place as a result of density differences caused by temperature gradients). Convection coefficients (hc) may be estimated for a number of simple geometries using correlations of data from experimental studies. These studies utilize appropriate dimensionless parameters to correlate results. Incropera and DeWitt present a number of these correlations in their text "Fundamentals of Heat and Mass Transfer." These correlations are also summarized in the ASTM Standard Practice C680, and in the ASHRAE Handbook—Fundamentals.
Controlling Surface Temperatures
A common calculation associated with mechanical insulation systems involves determining the thickness of insulation required to control the surface temperature to a certain value given the operating temperature of the process and the ambient temperature. For example, it may be desired to calculate the thickness of tank insulation required to keep the outside surface temperature at or below 140°F when the fluid in the tank is 450°F and the ambient temperature is 80°F.
At steady state, the heat flow through the insulation to the outside surface equals the heat flow from the surface to the ambient air. In equation forms #7, 8 and 9:
|
qins = qsurf |
(7) |
Or
|
(k/X)·A·(Thot–Tsurf) = h·A·(Tsurf–Tamb) |
(8) |
Rearranged, this equation yields:
|
X = (k/h)·[(Thot–Tsurf)/(Tsurf–Tamb)] |
(9) |
Since the ratio of temperature differences is known, the required thickness can be calculated by multiplying by the ratio of the insulation material conductivity to the surface coefficient.
In the example above, assume the surface coefficient can be estimated as 1.0 Btu/h ft2 °F, and the conductivity of the insulation to be used is 0.25 Btu-in/h ft2 °F. The required thickness can then be estimated as:
X = (0.25/1.0) [(450-140)/(140-80) = 1.29 in.
This estimated thickness would be rounded up to the next available size, probably 1‑½".
For radial heat flow, the thickness calculated would represent the equivalent thickness; the actual thickness (r2-r1) would be less—see Equation (8).
This simple procedure can be used as a first-order estimate. In reality, the surface coefficient is not constant but varies as a function of surface temperature, air velocity, orientation, and surface emittance.
When performing these calculations, it is important to use the actual dimensions for the pipe and tubing insulation. Many (but not all) pipe and tubing insulation products conform to dimensional standards originally published by the military in MIL-I-2781, and since adopted by other organizations, including ASTM. Standard pipe and insulation dimensions are given for reference in .
For mechanical insulation systems, it is also important to realize that the thermal conductivity (k) of most insulation products varies significantly with temperature. Manufacturers’ literature will usually provide curves or tabulations of conductivity versus temperature. When performing heat transfer calculations, it is important to utilize the "effective thermal conductivity," which can be obtained by integration of the conductivity versus temperature curve, or (as an approximation) utilizing the conductivity evaluated at the mean temperature across the insulation layer. ASTM C680 provides the algorithms and calculation methodologies for incorporating these equations in computer programs.
These complications are readily handled for a variety of boundary conditions using available software, such as NAIMA’s 3E Plus® (www.pipeinsulation.org).
An example printout from the 3E Plus program is shown in Figure 1.
Figure 1. Sample Printout from NAIMA 3E Plus Program.
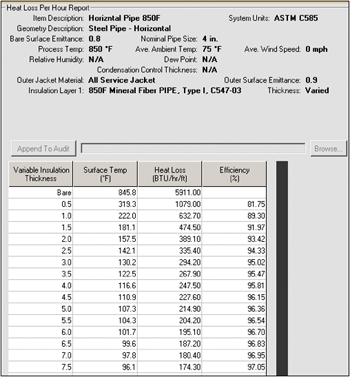
Estimates of the heat loss from standard pipe and tube sizes are given in Tables 6 and 7. These are useful for quickly estimating the cost of lost energy due to uninsulated piping.
Dimensions of Standard Pipe and Tubing Insulation
Table 2. Inner (ID) and Outer Diameters (OD) of Standard Pipe Insulation
| Pipe Size, NPS | Pipe OD, in. | Insulation ID, in. | Insulation Nominal Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1–½ | 2 | 2–½ | 3 | 3–½ | 4 | 4–½ | 5 | |||
| ½ | 0.84 | 0.86 | 2.88 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| ¾ | 1.05 | 1.07 | 2.88 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1 | 1.315 | 1.33 | 3.50 | 4.50 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1–¼ | 1.660 | 1.68 | 3.50 | 5.00 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1–½ | 1.900 | 1.92 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 |
| 2 | 2.375 | 2.41 | 4.50 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 |
| 2–½ | 2.875 | 2.91 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 |
| 3 | 3.500 | 3.53 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 |
| 3–½ | 4.000 | 4.03 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 12.75 | 14.00 |
| 4 | 4.500 | 4.53 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 |
| 4–½ | 5.000 | 5.03 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 14.00 | 15.00 |
| 5 | 5.563 | 5.64 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 | 16.00 |
| 6 | 6.625 | 6.70 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 | 16.00 | 17.00 |
| 7 | 7.625 | 7.70 | — | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 | 16.00 | 17.00 | 18.00 |
| 8 | 8.625 | 8.70 | — | 11.75 | 12.75 | 14.00 | 12.00 | 16.00 | 17.00 | 18.00 | 19.00 |
| 9 | 9.625 | 9.70 | — | 12.75 | 14.00 | 15.00 | 16.00 | 17.00 | 18.00 | 19.00 | 20.00 |
| 10 | 10.75 | 10.83 | — | 14.00 | 15.00 | 16.00 | 17.00 | 18.00 | 19.00 | 20.00 | 21.00 |
| 11 | 11.75 | 11.83 | — | 15.00 | 16.00 | 17.00 | 18.00 | 19.00 | 20.00 | 21.00 | 22.00 |
| 12 | 12.75 | 12.84 | — | 16.00 | 17.00 | 18.00 | 19.00 | 20.00 | 21.00 | 22.00 | 23.00 |
| 14 | 14.00 | 14.09 | — | 17.00 | 18.00 | 19.00 | 20.00 | 21.00 | 22.00 | 23.00 | 24.00 |
Table 3. Inner and Outer Diameters of Standard Tubing Insulation
| Tube Size, CTS | Tube OD, in. | Insulation ID | Insulation Nominal Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1–½ | 2 | 2–½ | 3 | 3–½ | 4 | 4–½ | 5 | |||
| 3/8 | 0.500 | 0.52 | 2.38 | 3.50 | 4.50 | 5.56 | 6.62 | — | — | — | — |
| ½ | 0.625 | 0.64 | 2.88 | 3.50 | 4.50 | 5.56 | 6.62 | — | — | — | — |
| ¾ | 0.875 | 0.89 | 2.88 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1 | 1.125 | 1.14 | 2.88 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1–¼ | 1.375 | 1.39 | 3.50 | 4.50 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 1–½ | 1.625 | 1.64 | 3.50 | 4.50 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 |
| 2 | 2.125 | 2.16 | 4.00 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 |
| 2–½ | 2.625 | 2.66 | 4.50 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 |
| 3 | 3.125 | 3.16 | 5.00 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 |
| 3–½ | 3.625 | 3.66 | 5.56 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 |
| 4 | 4.125 | 4.16 | 6.62 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 |
| 5 | 5.125 | 5.16 | 7.62 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 | 16.00 |
| 6 | 6.125 | 6.20 | 8.62 | 9.62 | 10.75 | 11.75 | 12.75 | 14.00 | 15.00 | 16.00 | 17.00 |
Table 4. Inner and Outer Diameters of Standard Flexible, Closed-Cell Pipe Insulation
| Pipe Size, NPS | Pipe OD, in. | Insulation ID, in. | Insulation OD, in. | ||
|---|---|---|---|---|---|
| Insulation Nominal Thickness | |||||
| ½" | ¾" | 1" | |||
| ½ | 0.84 | .97 | 1.87 | 2.47 | 2.97 |
| ¾ | 1.05 | 1.13 | 2.03 | 2.63 | 3.13 |
| 1 | 1.315 | 1.44 | 2.44 | 2.94 | 3.44 |
| 1–¼ | 1.660 | 1.78 | 2.78 | 3.38 | 3.78 |
| 1–½ | 1.900 | 2.03 | 3.03 | 3.63 | 4.03 |
| 2 | 2.375 | 2.50 | 3.50 | 4.10 | 4.50 |
| 2–½ | 2.875 | 3.00 | 4.00 | 4.60 | 5.00 |
| 3 | 3.500 | 3.70 | 4.66 | 5.26 | 5.76 |
| 3–½ | 4.000 | 4.20 | 5.30 | 5.90 | 6.40 |
| 4 | 4.500 | 4.70 | 5.88 | 6.40 | 6.90 |
| 4–½ | 5.000 | — | — | — | — |
| 5 | 5.563 | 5.76 | 6.86 | 7.46 | 7.96 |
| 6 | 6.625 | 6.83 | 7.93 | 8.53 | 9.03 |
| 7 | 7.625 | — | — | — | — |
| 8 | 8.625 | 8.82 | 9.92 | 10.52 | — |
Table 5. Inner and Outer Diameters of Standard Flexible, Closed-Cell Tubing Insulation
| Tube Nominal Size, in. | Tube OD | Insulation ID, in. | Insulation OD, in. | ||
|---|---|---|---|---|---|
| Insulation Nominal Thickness | |||||
| ½" | ¾" | 1" | |||
| 3/8 | 0.500 | .600 | 1.500 | 1.950 | — |
| ½ | 0.625 | .750 | 1.650 | 2.150 | 2.750 |
| ¾ | 0.875 | 1.000 | 1.950 | 2.500 | 3.000 |
| 1 | 1.125 | 1.250 | 2.220 | 2.850 | 3.250 |
| 1–¼ | 1.375 | 1.500 | 2.500 | 3.100 | 3.500 |
| 1–½ | 1.625 | 1.750 | 2.750 | 3.350 | 3.750 |
| 2 | 2.125 | 2.250 | 3.250 | 3.850 | 4.250 |
| 2–½ | 2.625 | 2.750 | 3.750 | 4.350 | 4.750 |
| 3 | 3.125 | 3.250 | 4.250 | 4.850 | 5.250 |
| 3–½ | 3.625 | 3.750 | 4.850 | 5.450 | 5.950 |
| 4 | 4.125 | 4.250 | 5.350 | 5.950 | 6.450 |
Heat Loss from Bare Pipe and Tubing
Table 6. Heat Loss from Bare Steel Pipe to Still Air at 80°F, Btu/h·ft
| Nominal Pipe Size, in. | Pipe Inside Temperature, °F | ||||
|---|---|---|---|---|---|
| 180 | 280 | 380 | 480 | 580 | |
| ½ | 56.3 | 138 | 243 | 377 | 545 |
| ¾ | 68.1 | 167 | 296 | 459 | 665 |
| 1 | 82.5 | 203 | 360 | 560 | 813 |
| 1–¼ | 102 | 251 | 446 | 695 | 1,010 |
| 1–½ | 115 | 283 | 504 | 787 | 1,150 |
| 2 | 141 | 350 | 623 | 974 | 1,420 |
| 2–½ | 168 | 416 | 743 | 1,160 | 1,700 |
| 3 | 201 | 499 | 891 | 1,400 | 2,040 |
| 3–½ | 228 | 565 | 1,010 | 1,580 | 2,310 |
| 4 | 254 | 631 | 1,130 | 1,770 | 2,590 |
| 4–½ | 281 | 697 | 1,250 | 1,960 | 2,860 |
| 5 | 313 | 777 | 1,390 | 2,180 | 3,190 |
| 6 | 368 | 915 | 1,640 | 2,580 | 3,770 |
| 7 | 421 | 1,040 | 1,880 | 2,950 | 4,310 |
| 8 | 473 | 1,180 | 2,110 | 3,320 | 4,860 |
| 9 | 525 | 1,310 | 2,340 | 3,680 | 5,400 |
| 10 | 583 | 1,450 | 2,610 | 4,100 | 6,000 |
| 12 | 686 | 1,710 | 3,070 | 4,830 | 7,090 |
| 14 | 747 | 1,860 | 3,340 | 5,260 | 7,720 |
| 16 | 850 | 2,120 | 3,810 | 6,000 | 8,790 |
| 18 | 953 | 2,380 | 4,270 | 6,730 | 9,870 |
| 20 | 1,060 | 2,630 | 4,730 | 7,460 | 10,950 |
| 24 | 1,260 | 3,150 | 5,660 | 8,920 | 13,100 |
©American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.
Table 7. Heat Loss from Bare Copper Tube to Still Air at 80°F, Btu/h·ft
| Nominal Tube Size, in. | Tube Inside Temperature, °F | ||||
|---|---|---|---|---|---|
| 120 | 150 | 180 | 210 | 240 | |
| 3/8 | 10.6 | 20.6 | 31.9 | 44.2 | 57.5 |
| ½ | 12.7 | 24.7 | 38.2 | 53.1 | 69.2 |
| ¾ | 16.7 | 32.7 | 50.7 | 70.4 | 91.9 |
| 1 | 20.7 | 40.5 | 62.9 | 87.5 | 114 |
| 1–¼ | 24.6 | 48.3 | 74.9 | 104 | 136 |
| 1–½ | 28.5 | 55.9 | 86.9 | 121 | 158 |
| 2 | 36.1 | 71.0 | 110 | 154 | 201 |
| 2–½ | 43.7 | 86.0 | 134 | 187 | 244 |
| 3 | 51.2 | 101 | 157 | 219 | 287 |
| 3–½ | 58.7 | 116 | 180 | 251 | 329 |
| 4 | 66.1 | 130 | 203 | 283 | 371 |
| 5 | 80.9 | 159 | 248 | 347 | 454 |
| 6 | 95.6 | 188 | 294 | 410 | 538 |
| 8 | 125 | 246 | 383 | 536 | 703 |
| 10 | 154 | 303 | 473 | 661 | 867 |
| 12 | 183 | 360 | 562 | 786 | 1,031 |
©American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.
