K-Value, U-Value, R-Value, C-Value
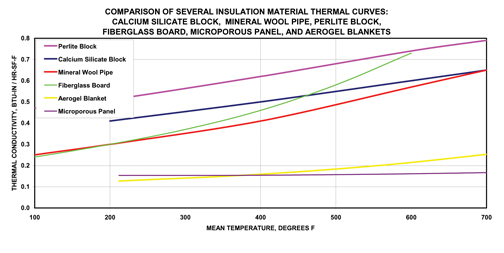
In most applications, the primary feature of a thermal insulation material is its ability to reduce heat exchange between a surface and the environment, or between one surface and another surface. This is known as having a low value for thermal conductivity. Generally, the lower a material’s thermal conductivity, the greater its ability to insulate for a given material thickness and set of conditions.
If it is really that simple, then why are there so many different terms, such as K-value, U-value, R-value, and C-value? Here is an overview with relatively simple definitions.
K-value
K-value is simply shorthand for thermal conductivity. The ASTM Standard C168, on Terminology, defines the term as follows:
Thermal conductivity, n: the time rate of steady state heat flow through a unit area of a homogeneous material induced by a unit temperature gradient in a direction perpendicular to that unit area.
This definition is really not that complex. Let’s take a closer look, phrase by phrase.
Time rate of heat flow can be compared to water flow rate, e.g., water flowing through a shower head at so many gallons per minute. It is the amount of energy, generally measured in the United States in Btus, flowing across a surface in a certain time period, usually measured in hours. Hence, time rate of heat flow is expressed in units of Btus per hour.
Steady state simply means that the conditions are steady, as water flowing out of a shower head at a constant rate.
Homogeneous material simply refers to one material, not two or three, that has a consistent composition throughout. In other words, there is only one type of insulation, as opposed to one layer of one type and a second layer of a second type. Also, for the purposes of this discussion, there are no weld pins or screws, or any structural metal passing through the insulation; and there are no gaps.
What about through a unit area? This refers to a standard cross-sectional area. For heat flow in the United States, a square foot is generally used as the unit area. So, we have units in Btus per hour, per square feet of area (to visualize, picture water flowing at some number of gallons per minute, hitting a 1 ft x 1 ft board).
Finally, there is the phrase by a unit temperature gradient. If two items have the same temperature and are brought together so they touch, no heat will flow from one to the other because they have the same temperature. To have heat flow by conduction from one object to another, where both are touching, there must be a temperature difference or gradient. As soon as there is a temperature gradient between two touching objects, heat will start to flow. If there is thermal insulation between those two objects, heat will flow at a lesser rate.
At this point, we have rate of heat flow per unit area, per degree temperature difference with units of Btus per hour, per square foot, per degree F.
Thermal conductivity is independent of material thickness. In theory, each slice of insulation is the same as its neighboring slice. The slices should be of some standard thickness. In the United States, units of inches are typically used for thickness of thermal insulation. So we need to think in terms of Btus of heat flow, for an inch of material thickness, per hour, per square foot of area, per degree F of temperature difference.
After picking apart the ASTM C168 definition for thermal conductivity, we have units of Btu-inch/hour per square foot per degree F. This is the same as the term K-value.
C-value
C-value is simply shorthand for thermal conductance. For a type of thermal insulation, the C-value depends on the thickness of the material; K-value generally does not depend on thickness (there are a few exceptions not in the scope of this article). How does ASTM C168 define thermal conductance?
Conductance, thermal, n: the time rate of steady state heat flow through a unit area of a material or construction induced by a unit temperature difference between the body surfaces.
ASTM C168 then gives a simple equation and units. In the inch-pound units used in the United States, those units are Btus/hour per square foot per degree F of temperature difference.
The words are fairly similar to those in the definition for thermal conductivity. What is missing is the inch units in the numerator because the C-value for a 2-inch-thick insulation board is half the value as it is for the same material 1-inch-thick insulation board. The thicker the insulation, the lower its C-value.
Equation 1: C-value = K-value / thickness
R-value
Typically, this term is used to describe the labeled performance rating of building insulation one can buy in a lumber yard. It is used less frequently for mechanical insulation, but it is still a useful term to understand. Its official designation is thermal resistance. This is how ASTM C168 defines it:
Resistance, thermal, n: the quantity determined by the temperature difference, at steady state, between two defined surfaces of a material or construction that induces a unit heat flow through a unit area.
ASTM C168 then provides an equation, followed by typical units. In the inch-pound units, thermal resistance is measured in degrees F times square feet of area times hours of time per Btus of heat flow.
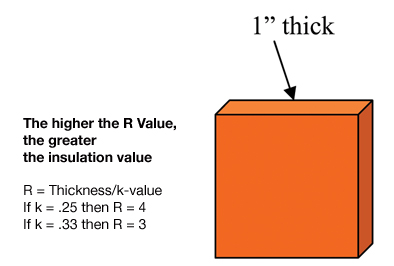
Most people know that for a given insulation material, the thicker it is, the greater the R-value. For example, for a particular type of insulation board, a 2-inch-thick board will have twice the R-value of the 1-inch-thick board.
Equation 2: R-value = 1 / C-value
If the C-value is 0.5, then the R-value is 2.0. One can calculate it from the equation for C-value in Equation 1 above:
Equation 3: R-value = thickness / K-value
Thus, if the thickness is 1 inch, and the K-value is 0.25, then the R-value is 1 divided by 0.25, or 4 (leaving off the units for brevity).
U-value
Finally, there is U-value, known officially as thermal transmittance. This is more of an engineering term used to designate the thermal performance of a system as opposed to a homogeneous material. The ASTM C168 definition is as follows:
Transmittance, thermal, n: the heat transmission in unit time through unit area of a material construction and the boundary air films, induced by unit temperature difference between the environments on each side.
There are a few new terms: the boundary air films and between the environments on each side. The previous definitions did not refer to environments.
The best way to illustrate thermal transmittance or U-value is through an example. Consider the wall of a typical insulated house with nominal 2 x 4 boards (which actually measure about 1-1/2 inches x 3-1/2 inches), spaced 16 inches on center, running vertically. One might see 3/8-inch-thick gypsum wall board on the inside of the wall, with a plastic film vapor barrier separating the gypsum wall board from the wood studs. Fiberglass batts may be filling the 3-1/2-inch-wide spaces between the 2 x 4 studs. On the outside of the studs, there might be 1/2-inch-thick polystyrene insulation boards covered with exterior wood sheathing. This example will ignore doors and windows, as well as the K-value and thickness of the plastic sheet used as the vapor barrier.
The calculation of the wall’s U-value is sufficiently complex to be beyond the scope of this article, but the following values must be known or at least estimated for its thermal transmittance to be calculated: *
- C-value of the indoor air film
- K-value of the 3/8-inch gypsum wall board
- K-value of the 3-1/2-inch-wide wood studs
- Spacing between the studs (16 inches, in this case)
- K-value of the fiberglass insulation batts, as well as their thickness (3-1/2 inches thick)
- Width of the fiberglass batts (16 inches minus the 1-1/2 inch thickness of the wood studs = 14-1/2 inches)
- K-value of the polystyrene boards and their thickness (1/2 inch)
- K-value and thickness of the wood siding materials
- C-value of the outdoor air film
The lower the U-value, the lower the rate of heat flow for a given set of conditions. A well-insulated building wall system will have a much lower U-value, or thermal transmittance, than an uninsulated or poorly insulated system.
To determine a mechanical insulation system’s U-value accurately, one must account for heat transfer through the homogeneous insulation as well as through any breaches and expansion gaps with a different insulation material. There is also the outside air film and occasionally an inside air film.
In reality, many non-homogenous portions are typically unaccounted for. The standard thermal conductivity test procedures typically treat the material as being homogeneous. In real applications, there are joints and sometimes cracks in rigid materials. These inconsistencies make the U-value greater than if the insulation behaved as a homogeneous material.
The concepts of K-value, C-value, R-value, and U-value can be summed up in the following rules:
- The better insulated a system, the lower its U-value.
- The greater the performance of a piece of insulation, the greater its R-value and the lower its C-value.
- The lower the K-value of a particular insulation material, the greater its insulating value for a particular thickness and given set of conditions.
These are the properties upon which users of thermal insulation depend for energy savings, process control, personnel protection, and condensation control.